Blockchain simulator - Merkle Tree 11
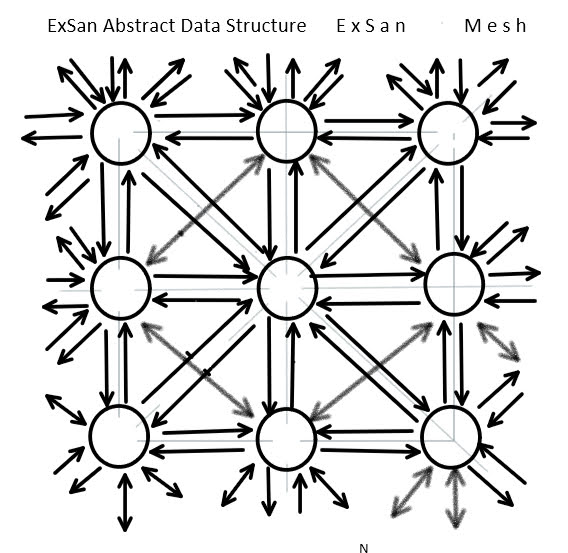
The ExSan Abstract Data Structure can be used to implement a complex blockchain structure.
Each ExSan Node can be considered a block in the chain, pointing to a Merkle Binary Tree.
In fact, each ExSan Node can point to any user-defined abstract structure.
1 LEARNING BLOCKCHAIN
2
This a Computer Science topic quite interesting.
3
I have coded my first simulations using ExSan
4
It already has implemented binary tree in every block / node
Wikipedia Merkle Tree
5
This simulations tracks blockchains transactions without hashing.
6
Every row is a peer, when it reaches the end of the row it comes
7
back to the begining of the row and keeps on.
8
COURSERA Bitcoin and Cryptocurrency Technologies
9
ref:
My Profile #opentowork
10
Code and output of the simulation of simple transactions as depicted on the picture above
11
1
2 ///----------CODE
3 /***********START***************/
4 void bckchxsn5() {
5 //nt number of nodes have been created already
6 //code should be modified to create merkle tree as it gets needed
7 // do not change this code it is just for test and promoting exsan
8 setJobID("bch5_");
9 string label = "Block Chain Simulator 5";
10 out("", label);
11
12 enum FLOAT { ppF };
13 enum BOOL { ppB };
14 enum USHORT { ppU };
15 enum STRING { ppW };
16 enum CHAR { ppC };
17
18 /// -----merkle Tree-------
19 ntNodes = 333; //magic number para crear nodos a medida que se necesiten
20 /// -----merkle Tree-------
21
22 unsigned short int nProc{ 15 };
23 unsigned short wtext{ 7 }, counToMerkel{ 0 }, wdt{ 3 }; //wdt display first and last wdt c
24 unsigned short rows{ 10 }, cols{ 10 }, lastActive{ 10 }; //always more than 1 here
25
26 double numDouble{ 0 };
27 char output[50];
28 string outputSt;
29
30 ///----
31 boost::random::uniform_int_distribution<> uniformRndInt{ 1, 99 }; //#include
32 boost::random::uniform_int_distribution<> uniformRndIntNBitCoins{ 0, 7 }; //#include
33 boost::random::uniform_int_distribution<> uniformRndIntTrueFals{ 0, 1 }; //#include
34 boost::random::uniform_int_distribution<> uniformRndIntTx{ 1, 5 };
35
36 unsigned seed = chrono::system_clock::now().time_since_epoch().count();
37 default_random_engine generator(seed);
38 unsigned short int nRollTheDice{ 33 };
39 ///----
40
41 NETPTR net{ nullptr };
42 CELLPTR ptr{ nullptr }, prevptr{ nullptr };
43
44 NODEPTR ptrN{ nullptr };
45 NODEPTR root_nt(nullptr);
46 NODEPTR ptr_new_node(nullptr);
47
48 ROWPTR rptr{ nullptr };
49 unsigned short int thisRow{ 0 }, thisCol{ 0 }, randNumber{ 0 };
50
51 rows = cols = 3;
52 net = net->exsan(rows, cols, ppF, ppB, ppU, ppW, ppC);
53 //* //test creating nt trees on demand
54 net->set_work_sheet(net, ppF, rows, cols);
55 /// generate a random number (0- 99) insert in the row+col node the number
56 // ej 33%9 = 6 row 3 col 3 insert 33
57 // insert number then traverse
58
59 boost::random::uniform_int_distribution<> uniformRndRC{ 1, rows };
60 fout << "\n\tLEDGER IN EVERY BLOCK - NODE";
61 const enum pages_nt { pp_lastIN, ppnt_time, ppnt_data, ppnt_medium }; // es necesario el
62 unsigned short* ary_ntPage = new unsigned short[ppnt_medium];
63 do {
64 randNumber = uniformRndInt(generator);
65 thisRow = uniformRndRC(generator); //ok
66 thisCol = uniformRndRC(generator); //ok
67
68 fout << "\n\n\tInsert randNumber: " << randNumber << " in Block Row: " << thisRow << "\tC
69 ptr = net->point_to(net, ppF, thisRow, thisCol, 'f');
70 ptr->set_data(ppF, randNumber);
71 ptr_new_node = ptr_new_node->create_Node();
72 ptr_new_node->set_key_nt((unsigned short)randNumber);
73 root_nt = ptr->get_ntHead();
74 ptr->RB_Insert_data_nt(ptr, root_nt, ptr_new_node); // the rb_tree
75 ptr->set_ntHead(root_nt);
76 fout << "\n\tTraverse parcial Merkel Tree in this node";
77 //ptr->Tree_Inorder_nt(ptr, root_nt, 0, 1); // indexAry = 0, display 1 )
78 out("", "inOrder"); hout << "<\p>"; ptr->Tree_Inorder_nt(ptr, root_nt, 1);
79 } while (--nRollTheDice);
80
81 fout << "\n\tVal in Block pp " << ppF; net->show_page(net, ppF, 'f', 0, 9, wtext + 2, 4 +
82 fout << "\n\tMerkel Tree in each block ";
83
84 if (1) {
85 rptr = net->goto_row(net, ppF, 1, 'f');
86 CELLPTR t;
87 for (thisRow = 1; thisRow <= net->get_rows_in_page(ppF, 'f'); thisRow++) {
88 ptr = rptr->get_forward_ptr();
89 for (thisCol = 1; thisCol <= net->get_cols_in_page(ppF, 'f'); thisCol++) {
90 if (!ptr->get_data(ppF)) { ptr = ptr->get_next_ptr(); continue; }
91
92 fout << "\n\n\tBlock [" << ptr->get_row() << ", " << ptr->get_col() << "]";
93 out("", "inOrder"); hout << "<\p>"; ptr->Tree_Inorder_nt(ptr, ptr->get_ntHead(), 1);
94
95 // ODEPTR head, unsigned short* aryPage, unsigned short ppnt_medium, unsigned short ntN
96 //ptr->Tree_Inorder_nt_TraverseAll(t, ptr->get_ntHead() , unsigned short* aryPage, unsi
97 //ptr->Tree_Inorder_nt_TraverseAll(ptr, ptr->get_ntHead(), ary_ntPage, ppnt_medium, ntN
98 ptr = ptr->get_next_ptr();
99 }
100 rptr = rptr->get_down_ptr();
101 }
102 }
103 net->kill_exsan(net);
104 return;
105 /***********END bkxsn3 Merkle Tree **********/
106
107
108 /////----------------output Merkle Tree
109 | ExSan | C++ | ExSan | MSVSC2019_V16_11.23@01.11
110 Tue Feb 7 09:46 : 44 2023
111
112 exsan.plusplus@gmail.com https ://twitter.com/#!/ExSan_com
113 JOB: bch5_4644
114
115 Block Chain Simulator 5
116 Generate Exsan(3, 3)
117
118 LEDGER IN EVERY BLOCK - NODE K = key in Merkel Tree node/block
119
120 Insert randNumber : 20 in Block Row : 2 Col : 3 try : 33
121 Traverse parcial Merkel Tree in this node
122 inOrder(2, 3)k-> 20
123
124 Insert randNumber : 91 in Block Row : 2 Col : 1 try : 32
125 Traverse parcial Merkel Tree in this node
126 inOrder(2, 1)k-> 91
127
128 Insert randNumber : 70 in Block Row : 1 Col : 1 try : 31
129 Traverse parcial Merkel Tree in this node
130 inOrder(1, 1)k-> 70
131
132 Insert randNumber : 39 in Block Row : 1 Col : 2 try : 30
133 Traverse parcial Merkel Tree in this node
134 inOrder(1, 2)k-> 39
135
136 Insert randNumber : 51 in Block Row : 2 Col : 1 try : 29
137 Traverse parcial Merkel Tree in this node
138 inOrder(2, 1)k-> 51 (2, 1)k-> 91
139
140 Insert randNumber : 41 in Block Row : 1 Col : 3 try : 28
141 Traverse parcial Merkel Tree in this node
142 inOrder(1, 3)k-> 41
143
144 Insert randNumber : 14 in Block Row : 1 Col : 3 try : 27
145 Traverse parcial Merkel Tree in this node
146 inOrder(1, 3)k-> 14 (1, 3)k-> 41
147
148 Insert randNumber : 28 in Block Row : 2 Col : 3 try : 26
149 Traverse parcial Merkel Tree in this node
150 inOrder(2, 3)k-> 20 (2, 3)k-> 28
151
152 Insert randNumber : 7 in Block Row : 2 Col : 1 try : 25
153 Traverse parcial Merkel Tree in this node
154 inOrder(2, 1)k-> 7 (2, 1)k-> 51 (2, 1)k-> 91
155
156 Insert randNumber : 53 in Block Row : 3 Col : 2 try : 24
157 Traverse parcial Merkel Tree in this node
158 inOrder(3, 2)k-> 53
159
160 Insert randNumber : 7 in Block Row : 2 Col : 2 try : 23
161 Traverse parcial Merkel Tree in this node
162 inOrder(2, 2)k-> 7
163
164 Insert randNumber : 68 in Block Row : 1 Col : 2 try : 22
165 Traverse parcial Merkel Tree in this node
166 inOrder(1, 2)k-> 39 (1, 2)k-> 68
167
168 Insert randNumber : 7 in Block Row : 1 Col : 2 try : 21
169 Traverse parcial Merkel Tree in this node
170 inOrder(1, 2)k-> 7 (1, 2)k-> 39 (1, 2)k-> 68
171
172 Insert randNumber : 25 in Block Row : 3 Col : 3 try : 20
173 Traverse parcial Merkel Tree in this node
174 inOrder(3, 3)k-> 25
175
176 Insert randNumber : 63 in Block Row : 2 Col : 2 try : 19
177 Traverse parcial Merkel Tree in this node
178 inOrder(2, 2)k-> 7 (2, 2)k-> 63
179
180 Insert randNumber : 80 in Block Row : 1 Col : 2 try : 18
181 Traverse parcial Merkel Tree in this node
182 inOrder(1, 2)k-> 7 (1, 2)k-> 39 (1, 2)k-> 68 (1, 2)k-> 80
183
184 Insert randNumber : 40 in Block Row : 1 Col : 3 try : 17
185 Traverse parcial Merkel Tree in this node
186 inOrder(1, 3)k-> 14 (1, 3)k-> 40 (1, 3)k-> 41
187
188 Insert randNumber : 89 in Block Row : 3 Col : 3 try : 16
189 Traverse parcial Merkel Tree in this node
190 inOrder(3, 3)k-> 25 (3, 3)k-> 89
191
192 Insert randNumber : 87 in Block Row : 3 Col : 3 try : 15
193 Traverse parcial Merkel Tree in this node
194 inOrder(3, 3)k-> 25 (3, 3)k-> 87 (3, 3)k-> 89
195
196 Insert randNumber : 26 in Block Row : 2 Col : 1 try : 14
197 Traverse parcial Merkel Tree in this node
198 inOrder(2, 1)k-> 7 (2, 1)k-> 26 (2, 1)k-> 51 (2, 1)k-> 91
199
200 Insert randNumber : 98 in Block Row : 2 Col : 2 try : 13
201 Traverse parcial Merkel Tree in this node
202 inOrder(2, 2)k-> 7 (2, 2)k-> 63 (2, 2)k-> 98
203
204 Insert randNumber : 69 in Block Row : 2 Col : 3 try : 12
205 Traverse parcial Merkel Tree in this node
206 inOrder(2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 69
207
208 Insert randNumber : 85 in Block Row : 3 Col : 1 try : 11
209 Traverse parcial Merkel Tree in this node
210 inOrder(3, 1)k-> 85
211
212 Insert randNumber : 53 in Block Row : 2 Col : 3 try : 10
213 Traverse parcial Merkel Tree in this node
214 inOrder(2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 53 (2, 3)k-> 69
215
216 Insert randNumber : 89 in Block Row : 2 Col : 2 try : 9
217 Traverse parcial Merkel Tree in this node
218 inOrder(2, 2)k-> 7 (2, 2)k-> 63 (2, 2)k-> 89 (2, 2)k-> 98
219
220 Insert randNumber : 71 in Block Row : 3 Col : 3 try : 8
221 Traverse parcial Merkel Tree in this node
222 inOrder(3, 3)k-> 25 (3, 3)k-> 71 (3, 3)k-> 87 (3, 3)k-> 89
223
224 Insert randNumber : 99 in Block Row : 2 Col : 3 try : 7
225 Traverse parcial Merkel Tree in this node
226 inOrder(2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 53 (2, 3)k-> 69 (2, 3)k-> 99
227
228 Insert randNumber : 80 in Block Row : 1 Col : 3 try : 6
229 Traverse parcial Merkel Tree in this node
230 inOrder(1, 3)k-> 14 (1, 3)k-> 40 (1, 3)k-> 41 (1, 3)k-> 80
231
232 Insert randNumber : 79 in Block Row : 2 Col : 3 try : 5
233 Traverse parcial Merkel Tree in this node
234 inOrder (2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 53 (2, 3)k-> 69 (2, 3)k-> 79
235 (2, 3)k-> 99
236
237 Insert randNumber : 27 in Block Row : 2 Col : 1 try : 4
238 Traverse parcial Merkel Tree in this node
239 inOrder(2, 1)k-> 7 (2, 1)k-> 26 (2, 1)k-> 27 (2, 1)k-> 51 (2, 1)k-> 91
240
241 Insert randNumber : 54 in Block Row : 3 Col : 2 try : 3
242 Traverse parcial Merkel Tree in this node
243 inOrder(3, 2)k-> 53 (3, 2)k-> 54
244
245 Insert randNumber : 40 in Block Row : 2 Col : 3 try : 2
246 Traverse parcial Merkel Tree in this node
247 inOrder(2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 40 (2, 3)k-> 53 (2, 3)k-> 69
248 (2, 3)k-> 79 (2, 3)k-> 99
249
250 Insert randNumber : 89 in Block Row : 3 Col : 3 try : 1
251 Traverse parcial Merkel Tree in this node
252 inOrder(3, 3)k-> 25 (3, 3)k-> 71 (3, 3)k-> 87 (3, 3)k-> 89 (3, 3)k-> 89
253 Val in Block pp 0
254 WORKSHEET 0 @[3, 3] FLOAT
255 A B C
256 > -------------------------- - <
257 1: 70 80 80
258 2: 27 89 40
259 3: 85 54 89
260 < --------------------------->
261
262 Merkel Tree in each block
263
264 Block[1, 1]
265 inOrder(1, 1)k-> 70
266
267 Block[1, 2]
268 inOrder(1, 2)k-> 7 (1, 2)k-> 39 (1, 2)k-> 68 (1, 2)k-> 80
269
270 Block[1, 3]
271 inOrder(1, 3)k-> 14 (1, 3)k-> 40 (1, 3)k-> 41 (1, 3)k-> 80
272
273 Block[2, 1]
274 inOrder(2, 1)k-> 7 (2, 1)k-> 26 (2, 1)k-> 27 (2, 1)k-> 51 (2, 1)k-> 91
275
276 Block[2, 2]
277 inOrder(2, 2)k-> 7 (2, 2)k-> 63 (2, 2)k-> 89 (2, 2)k-> 98
278
279 Block[2, 3]
280 inOrder (2, 3)k-> 20 (2, 3)k-> 28 (2, 3)k-> 40 (2, 3)k-> 53 (2, 3)k-> 69
281 (2, 3)k-> 79 (2, 3)k-> 99
282
283 Block[3, 1]
284 inOrder(3, 1)k-> 85
285
286 Block[3, 2]
287 inOrder(3, 2)k-> 53 (3, 2)k-> 54
288
289 Block[3, 3]
290 inOrder(3, 3)k-> 25 (3, 3)k-> 71 (3, 3)k-> 87 (3, 3)k-> 89 (3, 3)k-> 89
291
292 ENDS bch5_4644 Elapsed Time : 0.09 sec
293 Boost version : 1.80.0
294
295 EXIT FROM EXSAN
296
297
Polulating ExSan with Market Data Tick by Tick
Previous
Low Latency Systematic Trading Algorithm
Next
+
+
C
E
x
S
a
n
C
+
+
D
o
N
o
t
A
c
c
e
p
t
D
e
f
a
u
l
t
s
T
h
i
n
k
D
i
f
f
e
r
e
n
t